
Idriss Aberkane et la fumisterie mathématique
Une histoire narrée par Théodule la mule

Qui n'est en réalité nul autre que Vanessa Legrand-Apfelstrudel


Sommaire :
Hi-han, hi-han. Ah mince, j'ai été démasquée !
Comme vous le savez chers lecteurs, lorsque je tombe sur quelque chose qui m'énerve, je me sens obligé d'en faire un article de blog. Une forme de procédé cathartique sans doute. Jusqu'à présent, il a beaucoup été question de la dégringolade du niveaux académique avec les gender studies et autres fariboles dont nous gratifient le pays de l'oncle Sam. En revanche, ce qui me fout encore plus en rogne, c'est que des charlatans utilisent la corruption universitaire comme prétexte pour se donner légitimité, et accessoirement vendre quelques conférences au prix du caviar à des pigeons qui maîtrisent autant les sujets qu'eux (c'est-à-dire pas du tout). Il sera ainsi question aujourd'hui de ce très cher Idriss Aberkane, autorevendiqué hyperdocteur et mathématicien illustre à ses heures perdues, mais — Ô hélas ! — injustement persecuté par de fieffés profs d'universités bureaucrates corrompus qui s'obstinent à ne pas vouloir reconnaître son génie. Par pure jalousie à n'en point douter.
En ce qui concerne les mathématiques, j'avais déjà conscience du niveau de bullshit faramineux dont celui qui prétendait avoir résolu la conjecture de Collatz pouvait se montrer capable, mais je dois avouer que ce à quoi j'ai pu assisté a dépassé toutes mes espérances. "Conférence i", nommée ainsi en l'honneur de la fameuse unité imaginaire, a été publiée en Juillet 2020 sur sa chaîne Youtube. La première partie est consacrée à vulgariser la théorie des nombres, et la deuxième à présenter ses travaux de recherche sur ce qu'il appelle l'"algèbre romanesque", qu'il prétend avoir élaborée afin de démontrer la fameuse conjecture de Collatz. Une théorie dont la compréhension échappe encore à tout mathématiciens — autre qu'Aberkane j'entends — parce que ce sont tous des incompétents corrompus, faut-il le rappeler ?
Cette conférence, donc, se résume à un festival d'âneries, d'approximations, de non-sens et d'erreurs grossières (parfois niveau collège !). Inutile au passage d'aller consulter la section commentaire sous la vidéo puisqu'il semble que cette dernière aie été purgée de presque toute critique constructive. Ben voyons.
Quelle champ de cette illustre discipline en prendra le plus pour son grade ? C'est ce que nous allons découvrir au cours de cette fantastique épopée qui nous confrontera au terrible démon du pipotage et de l'ultracrépidarianisme, le redoutable empereur Hybris Genghis-Khan.
Il waconte que des Conway !
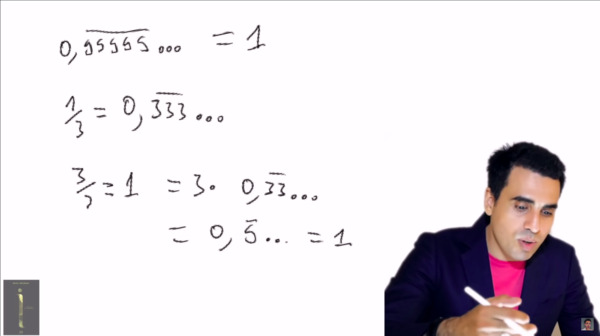
On commence donc avec la célèbre "preuve" du fait que \(0,99999\ldots= 1\). Je mets preuve entre guillemets car manipuler des parties fractionnaires infinies n'a rien de rigoureux en maths. "\(0\) avec une infinitié de \(9\) après la virgule" n'est rien d'autre qu'une représentation informelle d'un objet mathématique connu sous le nom de "série". Une preuve rigoureuse donnerait donc ceci :
Soit \(S\) la série définie par \(S = \sum_{k \geq 1} 9 \cdot 10^{-k}\). Cette série est évidemment convergente car géométrique de raison \(\frac{1}{10}\). On calcule donc : \[ S = 9 \sum_{k \geq 1} 10^{-k} = 9 \frac{\frac{1}{10}}{1 - \frac{1}{10}} = \frac{\frac{9}{10}}{\frac{9}{10}} = 1 \]
Vers l'infini et le dawa
Ce genre d'approximation n'est pas un cas isolé chez Aberkane, qui prouvera à mainte reprise qu'il ne comprends décidément rien à la notion de limite, entretenant une confusion totale entre ce qui est liées de près ou de loin à l'"infiniment petit" ou l'"infiniment grand" : cardinaux, ordinaux, symbole \(\infty\) (qui a une signification très précise en analyse), etc.
C'est ainsi qu'Idriss déclare que le \(dx\) dans la notation \(\frac{d}{dx}\) n'est en réalité nul autre que \(\epsilon\), l'infiniment petit de Conway. J'aurais bien demandé confirmation aux analystes si ils ne venaient pas tous de s'étouffer avec leur tartine de Nutella.

Apprenons donc l'analyse différentielle avec Idriss Aberkane :
\(dx = \epsilon\) vu que c'est une variation infinitésimale de \(x\). Ah oui, \(df(x) = \epsilon\) aussi, vu que c'est une variation infinitésimale de \(f(x)\). C'est tout petit, quoi. Ainsi : \[ \frac{df(x)}{dx} = \frac{\epsilon}{\epsilon} = 1\] Ce qui nous ammène donc au :
Théorème (Aberkane) : la dérivée de toute fonction \(C^1\) est constante égale à \(1\).
et donc :
Corollaire : toute fonction \(C^1\) est nulle.
Le screen suivant révèle à lui seul à peu près toute l'étendue de la confusion mentale de ce type. Mention spéciale à ces pauvres alephs passés à l'inverse bien malgré eux. La notion de cardinal semble lui avoir définitivement échappé.
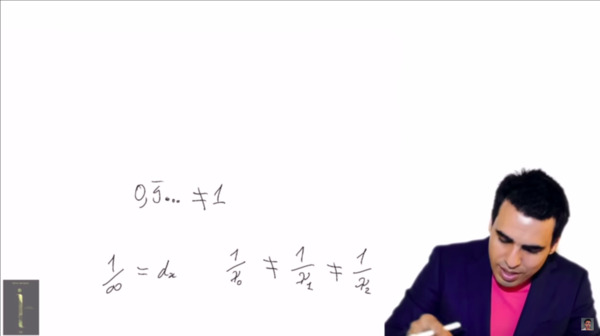
Toposophie
De toute les énormités qui sortent de la bouche d'Hydren, celle-ci figure probablement parmi mon top trois : si ce mec semble ne rien tilter à l'analyse, sa mécompréhension de la topologie s'avère plus effarante encore.

Bien entendu, il n'existe pas de telles bijections, même en y croyant très très fort (pour citer un de mes profs : "la méthode Coué, c'est bien, mais pas en maths"). Comme M. Aberkane semble porter une aversion toute particulière aux critiques non etayées, je vous en donne ici une preuve rigoureuse (vous pouvez passer si ça vous file de l'urticaire) :
Supposons qu'il existe une bijection continue \(f\) de \(\mathbb{R}\) dans \(\mathbb{R}^2\). Alors quel que soit \(n \geq 1 \), la restriction de \(f\) à l'intervalle \(I_n=[-n, n]\) est encore une bijection continue de \(I_n\) dans son image. Or \(I_n\) est compact, \(f(I_n)\) est Hausdorff donc \(f\vert_{I_n}\) est un homéomorphisme dans son image. En particulier, \(f(I_n)\) est un fermé de \(\mathbb{R}^2\), d'intérieur vide : en effet, si \(a\) est un point de l'intérieur de \(f(I_n)\), alors on peut trouver un petit voisinage ouvert \(U\) autour de \(a\) dans \(f(I_n)\). On note \(V := f^{-1}(U) \) voisinage ouvert de \(f^{-1}(a) \). Comme \(f^{-1}\) est continue sur \(U\), et \(U - a\) est connexe, \(f^{-1}(U-a)\) est nécessairement connexe. Mais \(f^{-1}(U-a) = V - f^{-1}(a)\) qui n'est pas connexe vu que \(V\) est un intervalle ouvert, donc l'intérieur de \(f(I_n)\) est vide. Donc : \[ \mathbb{R}^2 = f(\mathbb{R}) = f\left(\bigcup_{n \geq 1} I_n \right) = \bigcup_{n \geq 1} f(I_n) \] qui est un \(F_\sigma\) (union dénombrable de fermés d'intérieur vide) au vu de ce qui précède. Par le théorème de Baire, \(\mathbb{R}^2\) est d'intérieur vide, ce qui est absurde.
Il existe bien des courbes particulières qui recouvrent le plan (ou tout du moins le carré), comme celles de Peano ou Hilbert, cependant ces courbes s'autointersectent, il n'y a donc pas injectivité. D'ailleurs, Aberkane évoque les courbes de Hilbert juste après, ce qui confirme encore une fois sa méconnaissance totale du sujet.

On pourrait aussi parler du fait qu'il définisse l'ensemble des nombres réels comme l'ensemble des parties de \(\mathbb{N}\). Une pure hérésie dans la mesure où \(\mathbb{R}\) a vocation a être muni de sa topologie euclidienne. Allez donc définir la topologie euclidienne sur \(\mathscr{P}(\mathbb{N})\) ! C'est pourquoi \(\mathbb{R}\) est traditionnellement défini comme le complété de \(\mathbb{Q}\) pour la valeur absolue usuelle.

\(i\) comme inepte
On arrive ici à la partie sur les nombres imaginaires, qui pour le coup portent plutôt bien leur nom, vu l'imagination débordante dont fait preuve Aberkane lorsqu'il tente de les manipuler.
Ce dernier commence donc à définir \(i\) par "la racine de \(-1\)". Cette fois, c'est au tour des profs de prépa de tourner de l'oeil, car il ne faut pas perdre de vue que \(-1\) possède deux racines, \(i\) et \(-i\), donc écrire \(\sqrt{-1}\) me paraît somme toute cavalier. Néanmoins, cela reste un abus de notation assez courant, surtout pour de la vulga. Cependant, il confirmera son erreur un peu plus loin, en affirmant que \(i\) est LA racine du polynôme \(x^2+1\). Je tiens quand même à te signaler, cher Hydren, que \(x^2+1\) possède deux racines dans \(\mathbb{C}\), donc il aurait fallu dire "\(i\) est L'UNE des racines du polynôme \(x^2+1\)". Un détail sémantique somme toute anecdotique, bien qu'assez révélateur, surtout venant de quelqu'un qui affirme dans une autre de ses vidéos (24'17) qu'il juge Galois comme "le plus grand mathématicien du XIXe, devant Gauss, de très loin". Pour émettre un tel jugement, bien culotté au passage, il faudrait déjà au préalable avoir étudié la théorie de Galois, ou ne serait-ce que les rudiments de la théorie des extensions de corps. Ce lapsus ne présage rien de bon, et nos craintes vont bien vite se concrétiser, comme on le verra dans le chapitre suivant (je vous tease, eh oui).
Mais revenons à nos complexes, car une arnaque sauvage apparaît :

Une petite explication s'impose ici : dans les réels, l'écriture \(a^b\) est une abbréviation pour \(e^{b\ln(a)}\). Si l'on transpose ça aux complexes, on obtient : \(i^i = e^{iln(i)}\). Vous commencez à cerner le problème ? Le logarithme complexe n'a pas été défini au préalable ! Et pour cause : définir un logarithme sur \(\mathbb{C}\) consiste dans une tâche périlleuse, qui doit prendre en compte des considérations d'ordre topologique, or on a déjà pu constater les prouesses d'Abercrombie dans ce domaine. Allez hop, on cache la poussière sous le tapis, ni vu ni connu j'tembrouille, pour au final se retrouver à calculer un truc défini à la pisse. Rassurez-vous, ce n'est pas ça qui va arrêter Aberkane. Après tout, la rigueur ne semble pas l'étouffer outre mesure.

Il n'aura pas fallu attendre longtemps pour que les profs de prépa tombent définitivement de leur chaises. Genghis-Khan, toute honte bue, se met à appliquer des racines carrées de nombres complexes. En perdant de vue, une fois encore, que les nombres complexes admettent deux racines distinctes (sauf \(0\) bien entendu).
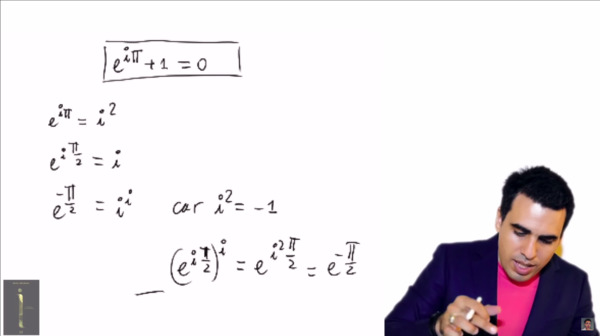
Bah oui, bien sûr, il suffit d'élever à la puissance \(i\) et tout s'arrange, CQFD ! D'une logique indéniable. Ça a tellement épaté les profs de prépa qu'ils viennent de s'étouffer dans leur propre vomi. D'ailleurs, comme le mentionne Aberkane, cette preuve est trouvable dans "n'importe quel cours d'algèbre de première année de fac, même fin lycée" (sic). On ne devait pas avoir les même références...
Esprit Galois
Les algébristes s'apprêtent à leur tour à bouffer les pissenlits par la racine, car une nouvelle perle se profile à l'horizon ! Selon Aberkane, \(\mathbb{C}\) est un corps algébriquement clos car ils est stable par les opérations élémentaires \(\left(+, -, \times, \div, ^2, \sqrt{} \right)\). Cette définition est malheureusement erronée : un corps \(\mathbb{K}\) est algébriquement clos si tout polynôme sur \(\mathbb{K}\) est scindé. Pour donner un contre-exemple, le corps fini à deux éléments \(\mathbb{F}_2\) est stable par toutes les opérations énumérées, mais n'est pas algébriquement clos vu que \(x^2+x+1\) n'est pas scindé.
On apprend peu après qu'Hydren n'est pas seulement ignorant, il ne sait pas non plus lire une page Wikipedia. Selon lui, le théorème fondamental de l'algèbre stipulerait que tout polynôme sur un corps \(\mathbb{K}\) algébriquement clos peut être résolu dans \(\mathbb{K}\), ce qui est on ne peut plus faux. C'est d'ailleurs tout l'objet de la fameuse théorie de Galois : à partir du degré \(5\), il n'est plus possible de résoudre les équations polynômiales par radicaux !
Cependant, c'est bien l'extrait à 1:03 qui aurait du fixer indéniablement et une bonne fois pour toute l'imposture intellectuelle d'Aberkane. Mais ce serait sous-estimer le pouvoir de nuisance de ce type : quoi que l'on fasse, ses abrutis de fans continueront à se prosterner devant le prétendu génie de ce charlatan, à se pâmer à l'écoute de ses élucubrations fumeuses, peu importe le nombre de preuve portées à son encontre, peu importe combien de Thomas Durand du dimanche s'acharneront à le debunker. Hélas pour eux le constat est sans appel : Idriss ne maîtrise pas les notions de base de première année de Licence !
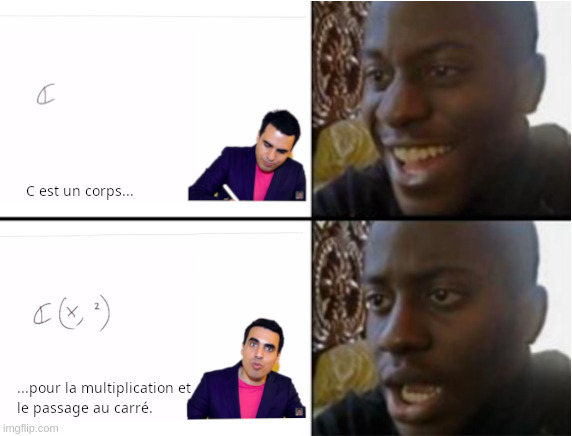
Affirmer que \((\mathbb{C}, \times, ^2)\) est un corps est non seulement absurde, vu que l'opération carrée n'est pas une loi de composition interne, en plus d'être faux, étant donné que \(0\) n'est pas inversible pour la loi \(\times\). Pour résumer, les compétences en algèbre d'Aberkane sont réduites là encore à néant.
Noggy style
Je trouve le passage sur les \(\log\) assez amusant en soi : le \(\log\) transformant la multiplication en addition, Aberkane se demande si il est possible de trouver un analogue du \(\log\) transformant la puissance en multiplication ? Une fonction qu'il choisit de noter... \(\nog\). Pourquoi pas après tout ?

A priori, rien n'assure l'existence d'une telle fonction (non triviale), cela me semble même mal barré vu que la puissance n'est pas commutative contrairement à la multiplication (ce qu'Aberkane pense tout de même à mentionner, mais sans plus). Par simple curiosité, analysons cette fameuse fonction \(\nog\), shall we ?
D'abord, \(\nog(a^b) = \nog(a)\nog(b) = \nog(b)\nog(a) = \nog(b^a)\). Prenons \(b=1\) : \(\nog(a^1) = \nog(1^a)\) donc \(\nog(a) = \nog(1)\)
Ainsi le \(\nog\) est constant sur \(\mathbb{R}\). Notons cette constante \(\alpha\). Il reste à trouver \(\alpha\). Or \(\nog(1^1) = \nog(1)\nog(1)\), d'où \(\alpha = \alpha^2\) donc \(\alpha = 0\) ou \(1\).
Ainsi, on se rend vite compte que le \(\nog\) est un concept complètement fumeux, vu que c'est soit la fonction nulle, soit la fonction constante égale à \(1\). Le \(\mog\) aussi par la même occasion, vu que le \(\mog\) est simplement le \(\log\) du \(\nog\), donc vaut nécéssairement \(0\). Mais d'après Aberkane, ce serait "exactement le genre de délires auxquels Conway se livrait". Idriss, je suis désolé, mais je doute que Conway portait un quelconque intérêt pour des trivialités de ce genre.
Arbres non-binaires
Après nous avoir récité de magnifiques poèmes et délivré d'innombrables anecdotes historiques dont je n'ai rien à carrer, Aberkane se décide enfin à aborder le cœur du sujet, à savoir ses "contributions" sur la conjecture de Collatz. Non peu fier de ses trouvailles, il dévoile devant nos yeux ébahis l'arbre binaire infini qui — Ô fait extraordinaire — comporterait une infinité non dénombrable de branches.
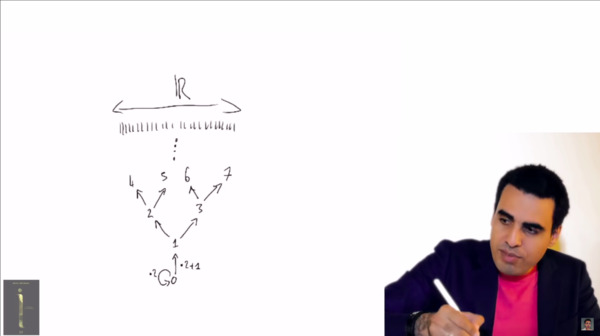
Il n'y a pas a dire, avec Aberkane, on n'est jamais déçu. Quand il ne raconte pas n'importe quoi, il se contente juste de réinventer l'eau tiède. Car ce que vous voyez là ne comporte rien de révolutionnaire, il s'agit simplement de la décomposition dyadique des nombres réels illustrée sous forme d'arbre binaire.
Mais voilà qu'arrive ce qui constitue probablement la plus grosse arnaque de ce séminaire. En effet, Aberkane prétend que les arbres infinis à 4 branches possèderaient un nombre de branche plus qu'indénombrable. Je vous laisse apprécier le calcul sur lequel il fonde son assertion :
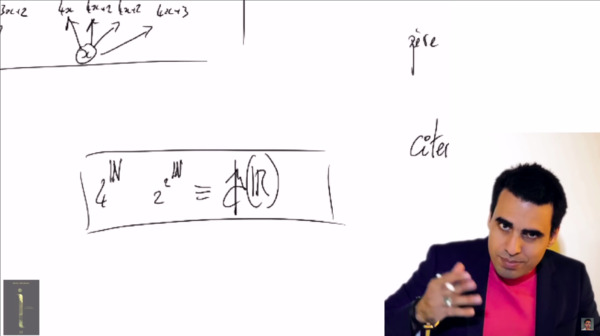
Amazing ! Wunderbar ! Sugoi desu ne ! Par un miracle inexplicable, l'exponentation est devenue commutative : \({(a^b)}^c = a^{(b^c)}\). C'est donc ça l'algèbre romanesque ? S'affranchir du carcan des règles de calcul traditionnelles, afin de repousser les frontières de la démonstration. Conway n'y aurait probablement jamais pensé, tiens. Mais hélas, cher Idriss, si tel est le cas, saches que tu n'es certainement pas pionnier dans cette discipline : en témoigne quiconque a déjà tenté de délivrer un cours de math à une classe de seconde.

Le reste de la présentation est incompréhensible. Si vous voulez perdre votre temps à essayer d'y biter quoi que ce soit (si tant est qu'il y aie quelque chose à comprendre), je vous laisse le lien vers le fameux article. Enjoy !
Conclusion
Dans la vidéo où Aberkane revendique sa résolution de Syracuse, celui-là n'hésite pas à se comparer à d'illustres mathématiciens tels que Grothendieck, Gauss ou encore Galois, tous génies incompris boycottés par le système. Et génie incompris, Aberkane, il se le revendique. Ses chevilles font la taille du système solaire. Il suffit de constater le degré de mépris dont il fait preuve lorsqu'il compare ses travaux à lui à ceux de Terence Tao : "Ca n'enlève rien au génie de Terence Tao, ce n'était juste pas un domaine dans lequel sa créativité et ses compétences pouvaient s'exprimer". Diantre ! L'arrogance de ce mec est stratosphérique.
Rendons ainsi hommage à toutes les victimes de ses odieuses calomnies, à tous ceux dont la réputation a été traînée dans la boue, à tous ceux qui se sont vu coller des procès pour diffamation, simplement pour avoir eu l'audace de dénoncer l'imposture de ce fumiste. Il y a fort à parier que si le principal intéressé tombe sur ce billet, il ne manquera pas d'hurler aux sophismes, de démentir avoir prononcé tel ou tel mot, ou encore d'invoquer la loi de Brandolini. L'hôpital qui se fout de la charité somme toute. Et bien entendu, ses quelques adeptes (de moins en moins nombreux j'ose l'espérer) s'acharneront encore et toujours à lui cirer les pompes. Pour ma part, je considère avoir accompli ma mission. Adios !

Commentaires
14 October 2025 à 14:35
Shol a écrit :
Ca fait du bien, merci